How to Find Inverse of a Matrix Using Numpy

In this post, we will learn how to find inverse of a matrix using numpy with detailed exaplanation and example.

Mathematically, the inverse of a matrix is only possible if it satisfies the following conditions:

1. The matrix should be a square matrix (the number of rows and columns must be the same)
2. The determinant of the matrix should be non-zero (det(A) ≠ 0), or you can say the matrix is non-singular.

Now let’s see the mathematical formula to calculate the inverse of the matrix first and then we jump into our programming part.

Formula to Find Inverse of a Matrix

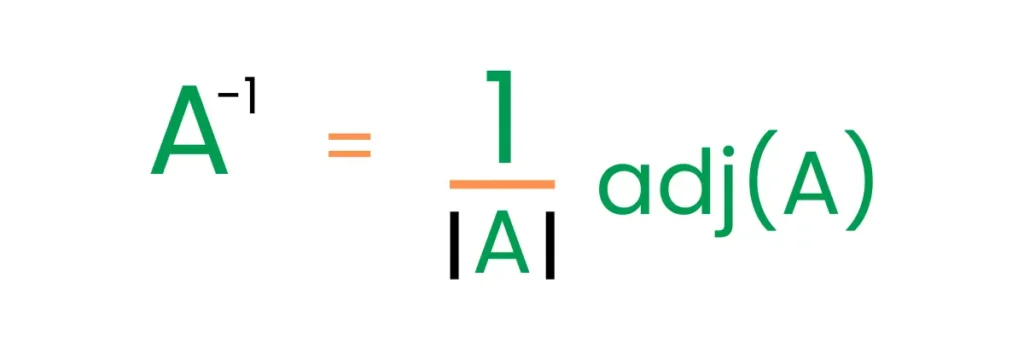
We are all set to jump into our programming part because we now have a basic understanding of how to calculate the inverse of a matrix.

All the above information is for your understanding. In the numpy library, there is one module called linalg (numpy.linalg). Inside that module, there is one built-in function called inv (numpy.linalg.inv()) that helps us to invert a matrix very easily in just one line. Let’s see a little more about this function.

numpy.linalg.inv()

The numpy.linalg.inv() function takes a matrix as input and returns the inverse of the matrix. It raises an error if the matrix is singular (non-invertible).

Syntax: numpy.linalg.inv(a). where a is your matrix.

Now, let’s write code to find the inverse of a matrix. But before diving into it, there are a few programming concepts you need to know:

1. How to take input from the user &
2. Numpy library

Source Code

import numpy as np

n = int(input("Enter size of a matrix: ")) # n x n

# Create matrix using numpy array
matrix = np.array([[int(input(f'column {j+1} -> Enter {i+1} element:')) for j in range(n)] for i in range(n)]) 

print("Matrix:")
print(matrix)

inv_matrix = np.linalg.inv(matrix) # inverse the matrix 

print("\nInverse of a Matrix:")
print(inv_matrix)

Output-1

Enter size of a matrix: 2
column 1 -> Enter 1 element:1
column 2 -> Enter 1 element:2
column 1 -> Enter 2 element:3
column 2 -> Enter 2 element:4
Matrix:
[[1 2]
 [3 4]]

Inverse of a Matrix:
[[-2.   1. ]
 [ 1.5 -0.5]]

Output-2

Enter size of a matrix: 3
column 1 -> Enter 1 element:1
column 2 -> Enter 1 element:2
column 3 -> Enter 1 element:1
column 1 -> Enter 2 element:2
column 2 -> Enter 2 element:4
column 3 -> Enter 2 element:7
column 1 -> Enter 3 element:8
column 2 -> Enter 3 element:3
column 3 -> Enter 3 element:9
Matrix:
[[1 2 1]
 [2 4 7]
 [8 3 9]]

Inverse of a Matrix:
[[ 0.23076923 -0.23076923  0.15384615]
 [ 0.58461538  0.01538462 -0.07692308]
 [-0.4         0.2        -0.        ]]

You can also verify your answer by checking A.A^-1 = I, here I is the identity matrix.

This is all about how we can find the inverse of a matrix using numpy. I hope this post adds some value to your life – thank you see you in the next article.