In this post, you will learn how to write a python program for the subtraction of two Matrices by taking input from the user with an example and algorithm.
Rule for Subtraction of two matrix
You can subtract two matrices if the number of rows and number of columns is the same for both the matrix.
Example:
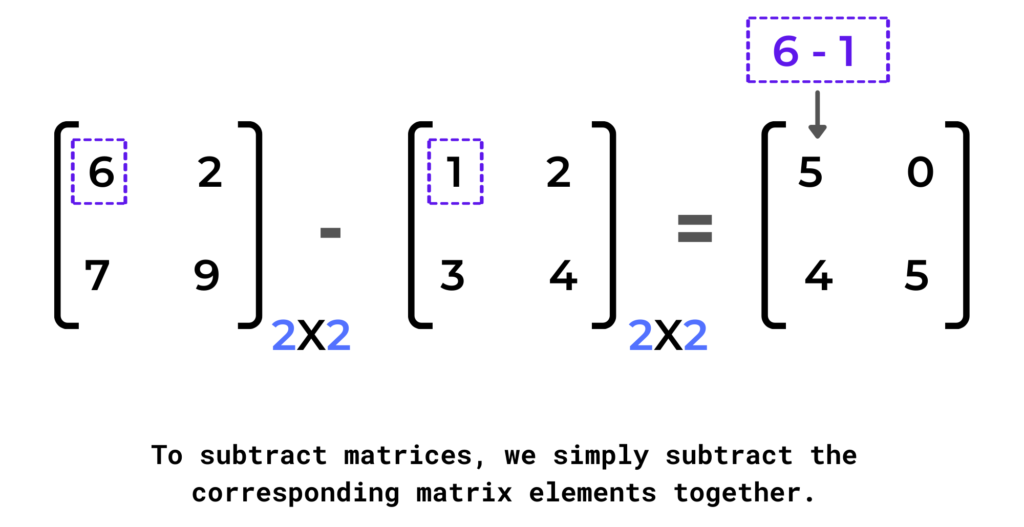
Algorithm for Subtraction of two matrices
| 1. | Ask the user for the input of rows (m) & columns (n) of the matrix. |
| 2. | Using input()function and list comprehension create matrix_A and matrix_B of dimension m x n. |
| 3. | For storing the result, create another matrix (result) of the same dimension m x n and initially, it is Zero. |
| 4. | Using nested for-loop do result[i][j] = matrix_A[i][j] - matrix_B[i][j] . |
| 5. | At last print the resultant matrix(result). |
Programming concepts you have to know for writing this program:
Source code
# matrix subtraction in python
rows = int(input('ENter number of rows: '))
cols = int(input('ENter number of column: '))
print() # for new line
print('Enter values for matrix A')
matrix_A = [[int(input(f"column {j+1} -> ENter {i+1} element:")) for j in range(cols)] for i in range(rows) ]
print() # for new line
print('Enter values for matrix B ')
matrix_B = [[int(input(f"column {j+1} -> ENter {i+1} element:")) for j in range(cols)] for i in range(rows) ]
print() #for new line
print('Matrix-A :')
for i in matrix_A:
print(i)
print() #for new line
print('Matrix-B :')
for i in matrix_B:
print(i)
# resultant matrix (matrix that store answer and intially it is Zero)
result = [[0 for j in range(cols)] for i in range(rows)]
# subtraction
for i in range(rows):
for j in range(cols):
result[i][j] = matrix_A[i][j] - matrix_B[i][j]
print() #for new line
print('Subtraction of Matrix-A and Matrix-B is :')
for i in result:
print(i)Output
ENter number of rows: 2
ENter number of column: 2
Enter values for matrix A
column 1 -> ENter 1 element:6
column 2 -> ENter 1 element:2
column 1 -> ENter 2 element:7
column 2 -> ENter 2 element:9
Enter values for matrix B
column 1 -> ENter 1 element:1
column 2 -> ENter 1 element:2
column 1 -> ENter 2 element:3
column 2 -> ENter 2 element:4
Matrix-A :
[6, 2]
[7, 9]
Matrix-B :
[1, 2]
[3, 4]
Subtraction of Matrix-A and Matrix-B is :
[5, 0]
[4, 5]





